Understanding the geometry of a comfortable staircase
Photo by Samuel Zeller on Unsplash
There was something I didn’t know about stairs
I’ve been following the rules for designing stairs for a long time.
But there’s a difference between knowing the rules and understanding them. Understanding them means knowing how and why they came about, their limitations, and how they might need to be interpreted in different circumstances.
In the case of stair design, I’d always intended to investigate a certain rule that I’d never really understood but never got around to. Then, one day, I did.
Basic staircase geometry
It doesn’t take much experience in planning buildings to realise that staircases take up a lot of space.
Exactly how much space a stair occupies is a function of the storey height, the form of the stair, and the stair geometry. Regarding stair geometry in the UK, the allowable step dimensions are controlled by the Building Regulations through the Approved Documents, in this case, Approved Document K: Protection From Falling, Collision and Impact.
You would naturally expect the regulations to control the height of the step (the rise), the depth of the tread (the going) and the overall steepness of the stair (the pitch angle), which they do.
In the current version of Approved Document K for England, the constraints for a private stair are:
Rise (r): must be between 150 and 220mm
Going (g): must be between 220 and 300mm
Pitch angle: anything up to a maximum of 42 degrees
But there is a further criterion, one which constrains the relationship between the going and riser, namely:
g+2r = 550mm to 700mm
I’ve always been aware of this equation. I’ve used it for all of the stairs I’ve designed, but if I’m honest, I’ve never really understood what it’s for, what it does or where it comes from. The Approved Document states it as a requirement but gives no explanation.
Why would you add two dimensions at right angles together? Why twice the rise? And where does the 550mm to 700mm range come from? I couldn’t guess what was behind it.
So, I decided to find out.
References to Blondel
It didn’t take much Google searching (e.g. ‘relationship between rise and going’) to establish that the g+2r equation is attributed to a 17th-century French architect named Francois Blondel.
I found plenty of references to him but no explanation for how he derived the equation or what was behind it. Along the way, I discovered that versions of the equation are used in many countries worldwide, and I wondered whether the relationship was universally applicable.
Some more searching led me to Blondel’s book, Cours d’Architecture, from 1675, and I found an online archive copy of the original. My schoolboy knowledge of French led me to the Chapter on ‘Escalier’, and then, with a little help from Google Translate, I managed to make sense of his thinking.
First of all, he refers to various other famous architects who came before him and who considered the design of the perfect stair. Pythagoras, Vitruvius, Scamozzi etc. He gives them short shrift and says that they were wrong.
Then, he gives his own thinking, which is summarised in this extract (my raw translation):
“The length of a comfortable step of a man who walks on the level is two feet, that is to say, twenty-four inches and the height of the step of a man who climbs a ladder erected is only a foot or twelve inches. From this, it appears that the natural length of the level step is double that of the natural height of the same in the vertical. Therefore to join them with each other, as done in a ramp, it is necessary that each part in height is compensated for by two parts of level and that both together compose a natural step of two feet or twenty-four inches long.”
“For this purpose, if in a ramp you have one inch of height to the step, it will be necessary to have twenty-two inches in width, because the twenty-two inches of level, with the height which is worth two inches in level, together make the length of the natural step of twenty-four inches. At three inches in height, the level step is eighteen inches wide. At four inches in height, the level step is sixteen inches wide. At five inches in height, fourteen inches of tread. Six inches high, twelve inches wide. At seven high, ten wide. At eight high, eight inches wide, and so on. What happens to be a perfectly good experience.”
So Blondel describes his theory but doesn’t write it as an equation.
He establishes that an average stride length is 24 inches on the horizontal. He recognises that if you are going to go up as well as a long, then the horizontal travel distance should be reduced to allow for the vertical rise. He realises that the dimension between ladder rungs is 12 inches and that this is half of the average stride length. Hence he concludes that the horizontal length should be reduced by double the vertical rise.
Which results in the formula: g + 2r = 24 inches
Which is such that when r = 0, g=24 inches. And when g= 0, r=12 inches.
Hang on a minute
The average stride length must vary.
And there must be variability in the dimension between ladder rungs.
For instance, my stride length is approximately 28 inches and measuring the ladders that I could find, I established that they varied from 8.5 inches to 10.5 inches. I couldn’t find any that had rung spacings of 12 inches.
With these variables, it is possible for the relationship between going and riser to be more like a factor of three.
So, was he correct?
People’s stride length varies, and the relationship between horizontal and vertical movement is also probably variable. Hence, it would be impossible, in reality, to arrive at a universally applicable relationship.
A better question would be, is his relationship useful? The fact that it has been used down the centuries since he derived it seems to indicate that it is. It appears to be good enough.
And when you equate it to a dimensional range rather than a specific dimension, it becomes more meaningful.
24 inches is 610mm, roughly in the middle of the 550mm to 700mm quoted in Approved Document K.
What the equation does
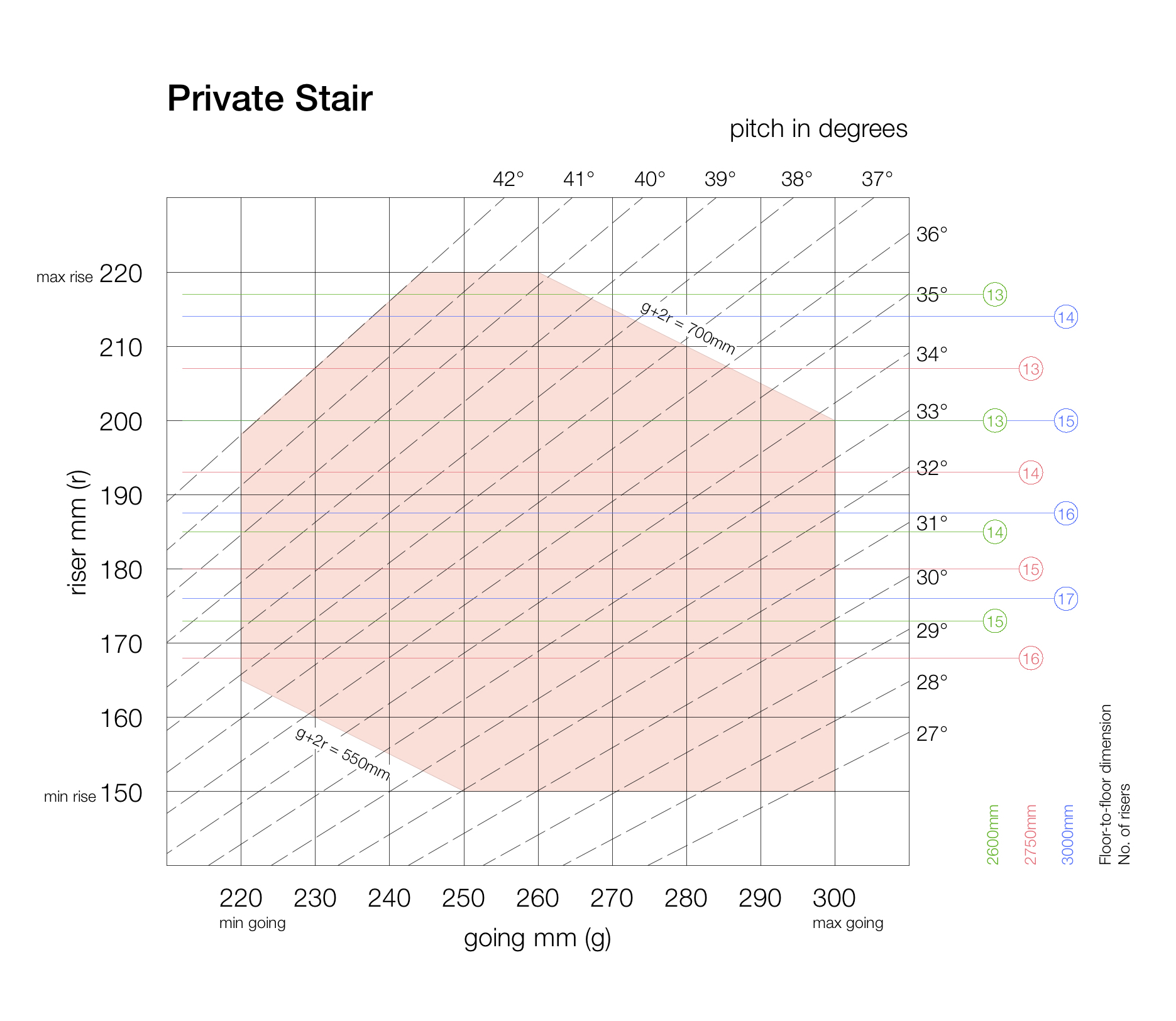
This is best visualised in a graph.
Allowable step geometries (pink area) from AD: K (2013) for private stair in England only.
This shows the allowable ranges of going and riser for a private stair (in England) and the resulting pitch angle (up to the maximum of 42 degrees).
The g + 2r relationship is a straight line plotted for 550mm and 700mm.
You can see that the Blondel equation, used in conjunction with a range, eliminates the extreme step geometries. You can’t have a short tread with a small rise and a long tread with a large rise.
In other words, the equation prevents people from having to take tiny steps or overly large strides. It keeps the stride length within a range generally accepted as comfortable.
How does this help?
Blondel’s relationship is designed to keep the stair geometry comfortable by limiting the stride length to an acceptable range. In doing so, it also helps to make the stairs safer.
But, having investigated the background of the equation, does my new-found knowledge about stair geometry improve my ability to design stairs? Has it made me a better architect?
Well, yes. A bit.
Previously, I would want a stair to comply, and I thought that steepness was the principal factor determining comfort and safety.
The graph provides a sense of how well a particular stair complies, and I would probably want a stair to be mid-range rather than approaching the extremes of the range of the Blondel equation.
It has also made me think more about how people perceive stairs. For instance, when designing a new house for someone, I’d want to know the geometry of their old house's stairs to help judge the new stairs.
If I were designing for young children or the elderly, I would think more carefully about the stride length and the pitch angle.
In certain circumstances, I would involve clients in decisions about the trade-off between the amount of space a stair takes up and comfort/safety.
Final word
In a previous article, I wrote about how we take aspects of our actions for granted. Digging deeper into selected knowledge areas can be fascinating and extremely beneficial. Why are you doing it like that?